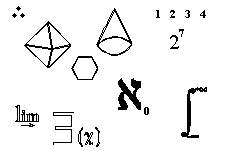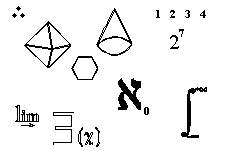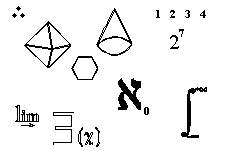
As if the existence of the Mind were not problematic enough, it raises the further issue of the apparent "contents" of the Mind—the things that we typically call ideas. Do ideas exist? They certainly seem to have a power all their own. Consider, for instance, the idea of Idealism itself, or of Communism, or of any of the other sorts of social -isms. No one can deny the power these ideas possess in their own right. Does this mean that we must admit that they, too, exist? And if they do, what kind of things are they?
Admittedly, all this talk about the existence of ideas is meant to be merely a stimulus to further research. Nevertheless, some philosophers do believe in the existence of certain ideas, and with good reason. For instance, the objects of mathematics—things like sets, groups, rings, and fields—are classic examples of ideas, though they would seem to most non-mathematicians to be only ideas, and nothing more. Still, most mathematicians act as if they were real, in some sense of the word. And so philosophers could—and a good many in fact do—insist upon the actual existence of mathematical objects.
This particular ontological position, known as Platonism, is very popular among both mathematicians and philosophers. They ask such questions as: "What esactly are Numbers, and do they exist in their own right?" An especially problematic kind of number, for instance, are the Transfinite Numbers, infinite numbers or various sizes. But even about such physical things as a pyramid, they ask "Does the mathematical equivalent of this, half an octahedron and necessarily an idea, exist in its own right?" If not, we might wonder, how we ever conceive of such unnatural objects. And finally, mathematicians ask a question that is of special interest to them, because it is one of the most basic question of all for mathematicians, and that is "What is a Set?"