Introduction to Statistics Course MATH 1342
Partial
Solutions to Chapters 4-5 Review Packet
Problem #3, Chapters 4-5 Review
Assume that there is a 0.15
probability that a basketball playoff series will last four games, a 0.30
probability that it will last five games, a 0.25 probability that it will last
six games, and a 0.30 probability that it will last seven games. Is it unusual for a team to win a series in 5
games?
This question contains info for a discrete probability
distribution. (The situation is not binomial because there are more than two
ways the series can play out.) Check that the sum of all probabilities = 1, a
requirement for probability distribution.
To classify a 5-game series as unusual (i.e., less than m-2s or
greater than m+2s), observe that we need to first
find m ands. Formulas 4-1 and 4-4 for any
discrete probability distribution apply in this case.
To
organize our arithmetic, let’s use a table:
|
Category
-> |
x |
P(x) |
x * P(x) |
x2 |
x2
* P(x) |
|
|
4 |
0.15 |
0.6 |
16 |
2.4 |
|
|
5 |
0.30 |
1.5 |
25 |
7.5 |
|
|
6 |
0.25 |
1.5 |
36 |
9.0 |
|
|
7 |
0.30 |
2.1 |
49 |
14.7 |
|
TOTAL (å) |
Not
needed |
1.00 |
5.7 |
Not
needed |
33.6 |
Thus, according to formulas 4-1 and 4-4 in the textbook, m =
5.70 s » 1.0536.
And m-2s » 3.59 and m+2s » 7.81.
A 5-game series is within this range (i.e., 3.59<5<7.81), and should not
be considered unusual.
There is no direct TI-83 function or button to compute m and s for
general probability distributions. However, the TI calculator can be very big
help in an indirect fashion. For example, you may certainly use the list editor
on the TI calculator to help organize, multiply and sum the various quantities.
Problem #4, Chapters 4-5 Review
A survey for brand
recognition is done and it is determined that 68% of consumers have heard of
Dull Computer Company. A survey of 800 randomly selected consumers is to be
conducted. For such groups of 800, would it be unusual to get 626 consumers who
recognize the Dull Computer Company name?
This question concerns a binomial probability situation.
Either a consumer has or has not heard of the Dull Computer Company.
To classify this set of 626 consumers as unusual (i.e.,
less than m-2s or greater than m+2s),
observe that we need to first find m and s. Formulas 4-6 and 4-8 for a
binomial probability distribution apply in this case.
According to formulas 4-6 and 4-8, we need to first establish
values for n, p, and q. We are given that n = 800, and that p = 0.68. Thus, q = 1 –
0.68 = 0.32.
Applying formulas 4-6 and 4-8 for m and s, we
have:
![]()
And finally, m-2s » 518 and m+2s » 570. Because
626 > 570, the max “usual” value, we conclude that it would be unusual to
find a set of 626 consumers who recognize the Dull Computer Company.
Problem #6, Chapters 4-5 Review
Find the probability of at least 2 girls in 9 births.
Assume that male and female births are equally likely and that the births are
independent events
We discussed this solution method on the TI-83 in class:
1 - binomcdf(9,.5,1) » 0.980
A student asked if the solution method would be the same if
we were asked to find the probability of getting at least 1 girl in 9 births.
Yes, the general solution method would be the same.
On the TI-83 calculator, you would enter:
1 - binomcdf(9,.5,0) » 0.998
Problem #32, Chapters 4-5 Review
A final exam in Math
160 has a mean of 73 with standard deviation 7.8. If 24 students are randomly
selected, find the probability that the mean
of their test scores is greater than
78.
Because we are asked to find the probability of
a certain mean, the Central Limit Theorem (CLT) applies. We are asked: what is
the probability that the mean test score is greater than 78?
The sample size n = 24 is relatively small (i.e., less than 30), but we will make a
simplifying assumption that the original test score data is normally distributed.
Thus, the CLT still applies (refer to the discussion on the bottom of p.260).
And so, we need to find P(x>78) = ?
To solve this problem using Table A-2, we need
to select the correct transformation formula to convert our “x” data to the z-scale:
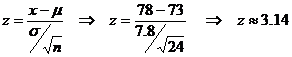
Observe that we divided by the Ö24 because we are using the CLT.
According to Table A-2, a z-value of 3.14 corresponds to an area of 0.9992 for the region to
the left of z = 3.14
However, remember that we are asked to find the
probability of being greater than
some value, that is, we must find the area to the right of our z-value.
We know that the total area under the normal
curve (and for any probability distribution curve) must = 1. Thus:
Area to the left of z
= 3.14 and the
Area to the right of z = 3.14 must = 1.
Substituting the appropriate algebra notation,
we have:
0.9992 + P(z>3.14) =
1 or
P(z>3.14) = 1 – 0.9992 = 0.0008
So the probability of getting a mean test score
greater than 78 is approximately 0.0008.
******************************************************************************
Alternatively, here is the solution method using
the TI-83 calculator:
normalcdf(78,10000,73,7.8/Ö24) » 0.0008
Note that we use 10000 as the approximate right
boundary to the region starting at x
=78 and increasing toward positive infinity.